250x250
반응형
Notice
Recent Posts
Recent Comments
Link
N
(백준 c++) 2580 스도쿠 본문
728x90
반응형
문제
스도쿠는 18세기 스위스 수학자가 만든 '라틴 사각형'이랑 퍼즐에서 유래한 것으로 현재 많은 인기를 누리고 있다. 이 게임은 아래 그림과 같이 가로, 세로 각각 9개씩 총 81개의 작은 칸으로 이루어진 정사각형 판 위에서 이뤄지는데, 게임 시작 전 몇 몇 칸에는 1부터 9까지의 숫자 중 하나가 쓰여 있다.

나머지 빈 칸을 채우는 방식은 다음과 같다.
- 각각의 가로줄과 세로줄에는 1부터 9까지의 숫자가 한 번씩만 나타나야 한다.
- 굵은 선으로 구분되어 있는 3x3 정사각형 안에도 1부터 9까지의 숫자가 한 번씩만 나타나야 한다.
위의 예의 경우, 첫째 줄에는 1을 제외한 나머지 2부터 9까지의 숫자들이 이미 나타나 있으므로 첫째 줄 빈칸에는 1이 들어가야 한다.

또한 위쪽 가운데 위치한 3x3 정사각형의 경우에는 3을 제외한 나머지 숫자들이 이미 쓰여있으므로 가운데 빈 칸에는 3이 들어가야 한다.

이와 같이 빈 칸을 차례로 채워 가면 다음과 같은 최종 결과를 얻을 수 있다.
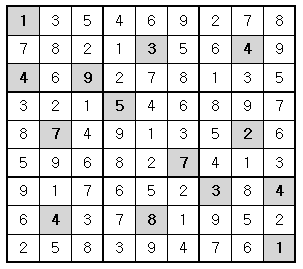
게임 시작 전 스도쿠 판에 쓰여 있는 숫자들의 정보가 주어질 때 모든 빈 칸이 채워진 최종 모습을 출력하는 프로그램을 작성하시오.
입력
아홉 줄에 걸쳐 한 줄에 9개씩 게임 시작 전 스도쿠판 각 줄에 쓰여 있는 숫자가 한 칸씩 띄워서 차례로 주어진다. 스도쿠 판의 빈 칸의 경우에는 0이 주어진다. 스도쿠 판을 규칙대로 채울 수 없는 경우의 입력은 주어지지 않는다.
출력
모든 빈 칸이 채워진 스도쿠 판의 최종 모습을 아홉줄에 걸쳐 한 줄에 9개씩 한 칸씩 띄워서 출력한다.
스도쿠 판을 채우는 방법이 여럿인 경우는 그 중 하나만을 출력한다.
#include <iostream>
using namespace std;
int board[9][9];
bool R[9][9];
bool C[9][9];
bool NN[9][9];
void dfs(int count)
{
int row = count / 9;
int col = count % 9;
if (count == 81)
{
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
cout << board[i][j] << " ";
}
cout << endl;
}
exit(0);
}
if (board[row][col] == 0)
{
for (int i = 1; i <= 9; i++)
{
if (!R[row][i] && !C[col][i] && !NN[(row / 3) * 3 + (col / 3)][i])
{
R[row][i] = true;
C[col][i] = true;
NN[(row / 3) * 3 + (col / 3)][i] = true;
board[row][col] = i;
dfs(count + 1);
R[row][i] = false;
C[col][i] = false;
NN[(row / 3) * 3 + (col / 3)][i] = false;
board[row][col] = 0;
}
}
}
else
dfs(count + 1);
}
int main()
{
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
cin >> board[i][j];
if (board[i][j] != 0)
{
R[i][board[i][j]] = true;
C[j][board[i][j]] = true;
NN[(i / 3) * 3 + (j / 3)][board[i][j]] = true;
}
}
}
dfs(0);
return 0;
}728x90
반응형
'백준 알고리즘' 카테고리의 다른 글
| (백준 c++)17413 단어뒤집기2 (0) | 2020.12.27 |
|---|---|
| (백준 c++)1935 후위표기식2 (0) | 2020.12.27 |
| (백준 c++) 9663 N-Queen (0) | 2020.09.21 |
| (백준 c++) 15652 N과 M(4) (0) | 2020.09.21 |
| (백준 c++) 15651 N과 M(3) (0) | 2020.09.21 |
